

新人のための電気の基礎知識(数学の基礎)
| 2.直流回路 2.1.オームの法則 2.2.電力・熱エネルギー 2.3.直流回路の計算 2.4.電源(電池)の接続 |
3.磁気 3.1.電流と磁気の関係 3.2.磁力・磁束 3.3.磁性体 3.4.電磁誘導 |
4.静電気・コンデンサ 4.1.電子・静電気 4.2.クーロンの法則 4.3.コンデンサ 4.4.コンデンサの接続 | 5.交流回路 5.1.正弦波交流 5.2.ベクトル 5.3.RLC回路 5.4.位相 |
6.三相交流 6.1.三相交流 6.2.三相結線 6.3.交流電力 6.4.三相四線式・単相三線式 |
|
| 進む |
| 複 素 数 |
実 数 |
有 理 数 |
整 数 |
+の整数(自然数) |  |
|||
| 0 | ||||||||
| −の整数 | ||||||||
| 分 数 |
真分数 仮分数 帯分数 |
有限小数 |
||||||
| 無限小数 (循環小数) |
||||||||
| 無理数(無限小数) | ||||||||
| 複素数 | ||||||||
| 面積 | 三角形の面積 | 底辺×高さ÷2 |  |
| 正三角形の面積 | √3÷4×a2 |  |
|
| 長方形の面積 | 底辺×高さ | ||
| 正方形の面積 | 辺2 | ||
| 平行四辺形の面積 | 底辺×高さ |  |
|
| 台形の面積 | (底辺+上辺)×高さ÷2 |  |
|
| 正六角形の面積 | ((3√3)/2)×r2=2.598r2 r:正六角形の外接円の半径 |
 |
|
| 円の面積 | πr2 r:半径 |
 |
|
| 扇型の面積 | (1/2)Lr L:弧の長さ r:弧の半径 |
 |
|
| 楕円の面積 | πab a:横軸の半径 b:縦軸の半径 |
 |
|
| 表面積・体積 | 角柱の表面積 | 側面積+2×底面積 |  |
| 角柱の体積 | 底面積×高さ | ||
| 円柱の表面積 | 側面積+2×底面積 =2πrh+2×πr2 r:底面の半径 |
 |
|
| 円柱の体積 | 底面積×高さ=πr2h r:底面の半径 |
||
| 正四面体の面積 | 4×(√3÷4×a2)=√3×a2 a:1辺の長さ |
 |
|
| 正四面体の体積 | (1/12)×√2×a3 a:1辺の長さ |
||
| 円錐の面積 | πr2+πr×√(r2+h2) |  |
|
| 円錐の体積 | (1/3)πr2h r:底面の半径 h:円錐の高さ |
||
| 球体の面積 | 4πr2 r:球の半径 |
 |
|
| 球体の体積 | (4/3)πr3 r:球の半径 |
||
| 分数計算の規則 | 分母と分子に同じ数をかけても、割っても値は等しい |
||
| 最小公倍数 | ・倍数 ある整数aを整数bで割り切れる時、整数aは整数bの倍数という。 例) ・16の倍数 16,32,48,64、80,96,112,128,144,160,・・・ ・18の倍数 18,36,54,72,90,108,144、162・・・ ・最小公倍数 2個以上の数に共通する倍数(公倍数)のうち、最も小さい公倍数を最小公倍数という 例)16と18の最小公倍数→144 |
||
| 最大公約数 | ・約数 ある整数aを割り切れる整数bを整数aの約数という。 例) ・16の約数 1,2,4,、8,16 ・24の約数 1,2,3,4,6,8,12,24 ・最大公約数 2個以上の数に共通する約数(公約数)のうち、最も大きな公約数を最大公約数という。 例)16と18の最大公約数→8 既約分数 |
||
| 逆数 | ある数・分数の分子と分母を逆転したものを言う。 |  |
|
| 繁分数 | |||
| 既約分数 | |||
| 約分 | 分数において、分子と分母を公約数で割る事を約分といい、 それ以上約分出来ない状態の分数を既約分数という。 分子と分母を最大公約数で割ることで既約分数化する。 |
 |
|
| 通分 | 2個の分数の、双方の分母の最小公倍数を、両方の分子と分母にかける事で、分母を同じ数にする。 | ||
| 四則演算 | 加算 | ・分母が同じ分数同士の加算 分母はそのままで、分子のみを加算する。 ・分数と整数 整数を分数の形に変換(同じ分母)したあと分子同士を加算する。 ・分母が異なる分数同士の加算 通分して分母を同じにした上で、分子を加算する。 加算後(演算中)、必要により約分する。 |
 |
| 減算 | ・分母が同じ分数同士の減算 分母はそのままで、分子のみを減算する。 ・分数と整数 整数を分数の形に変換(同じ分母)したあと分子同士を減算する。 ・分母が異なる分数同士の減算 通分して分母を同じにした上で、分子を減算する。 減算後(演算中)、必要により約分する。 |
 |
|
| 乗算 | ・分数と整数 分子のみに整数を乗算する。 ・分数と分数 分子と分子を乗算し、分母と分母を乗算する。 演算後(演算中)、必要により約分する。 |
 |
|
| 除算 | ・分数と整数 分母のみに整数を乗算する。 ・分数と分数 除算する分数の逆数を乗算する。 演算後(演算中)、必要により約分する。 |
 |
|
| 正比例 | y:xの時 比の値a=y/x 式を変形して y=ax この時、yはxに比例するといい、aを比例定数という。 |
 |
|
| 反比例 | y=a/xの時 yはxに反比例するという。 |
||
| 比例式 | 基本 |
a:b=x:yの時、 (b,xを内項、a,yを外項と称する) a/b=x/y 式を変形して ay=bx 内項の積は外項の積に等しい。 |
 |
| 分数関数式 | 例) (x+a)/(x−a)=(x−b)/(x−c) 式を変形して (x+a)(x−c)=(x−a)(x−b) →上記比例の式の変形と同じ 式を展開して x2−cx+ax−ac=x2−ax−bx+ab 右辺、左辺の共通項を整理・移行して x(2a+b−c)=a(b+c) x=a(b+c)/(2a+b−c) |
 |
|
| 連比式 | a:b=x:yの比の関係にあり、かつ、b:c=y:zの比の関係が成り立つとき、 a:b:c=x:y:zと表記する(連比式と称する) a:b:c=x:y:z等相似三角形の各辺の比の様な3以上の数の比の関係。 a/x=b/y=c/z |
 |
|
| 比例式の変形 | a/b=x/y ならば a/x=b/yが成立する。 |
 |
|
| 加比の理 | a/x=b/yならば、 a/x=b/y=(a+b)/(x+y)が成立する。 同様に、 a/x=b/y=c/zならば、 a/x=b/y=c/z=(a+b+c)/(x+y+z) |
 |
|
| 累乗・指数 | an=a×a×a×・・・n回 a-n=1/(an) |
||
| 累乗(指数)の四則演算 | 加算 | a(m+n)=am×an |  |
| 減算 | a(m-n)=am÷an |
||
| 乗算 | a(m×n)=(am)n | ||
| 除算 | a(m÷n)=n√(am) | ||
| 平方根 | b2=aの時 √a=bまたは-b |
||
| 平方根の四則演算 | 加算 | √a+√b=そのまま (√(a+b)にはならない) |
|
| 減算 | √a−√b=そのまま (√(a−b)にはならない) |
||
| 乗算 | √a×√b=√(a×b) |  |
|
| 除算 | √a÷√b=√(a÷b) | ||
| 混在式の有理化 | |||
| 対数(logarithm) | x=apの時(但し、a≠1) p=logax の形で表現する。 ・pを、aを底(base)とするxの対数 ・xを、真数(anti-ligarithm)という。 |
|
| 常用対数 | a(底)を10とした対数を常用対数という。(”Log”) y=log10x → x=10y 例) log102 =0.30103 → 10(0.30103) ≒2 log103 =0.47712 → 10(0.47712) ≒3 log104 =0.60206 → 10(060206) ≒4 log105 =0.69897 → 10(069897) ≒5 log106 =0.77815 → 10(0.77815) ≒6 log107 =0845098 → 10(0.845098)≒7 log108 =0.90309 → 10(0.90309) ≒8 log109 =0.95424 → 10(0.95424 )≒9 log1010=1 → 10(1) =10 log100.001=−3 log100.01=−2 log100.1=−1 log101=0 log1010=1 log10100=2 log101000=3 |
|
| logの公式 | log10(mn)=log10m+log10n log10(m/n)=log10m−log10n log10(mn)=n×log10m |
| 三角形の特徴 | 三角形の内角の和 | 三角形の内角の和は180度 |  |
||||||||||||||||||||||||
| 2等辺三角形 | 2辺の長さが等しい時、または内角2角が等しい時、その三角形を二等辺三角形という。 |  |
|||||||||||||||||||||||||
| 正三角形 | 3辺の長さが等しい時、又は、内角3角が等しい時、その三角形を正三角形という。 |  |
|||||||||||||||||||||||||
| 三角形の合同 | 複数の三角形の三辺が等しい |  |
|||||||||||||||||||||||||
| 複数の三角形の2辺と挟まれる角度が等しい | |||||||||||||||||||||||||||
| 複数の三角形の1辺と両端の角度が等しい | |||||||||||||||||||||||||||
| 直角三角形の合同 | 複数の直角三角形の斜辺と一つの鋭角が等しい |  |
|||||||||||||||||||||||||
| 複数の直角三角形の斜辺と他の1辺が等しい | |||||||||||||||||||||||||||
| 三角形の相似 | 複数の三角形の三辺の比が等しい |  |
|||||||||||||||||||||||||
| 複数の三角形の2辺の比と挟まれる角度が等しい | |||||||||||||||||||||||||||
| 複数の三角形の2組の角度が等しい | |||||||||||||||||||||||||||
| 三角形の重心 | △abcの3つの中線は1点で交わる その交点は重心を示す。 |
 |
|||||||||||||||||||||||||
| 三角形の内心 | △abcの各内角の二等分線は1点で交わる その交点は内接円の中心を示す。 |
 |
|||||||||||||||||||||||||
| 三角形の外心 | △abcの3辺の垂直2等分線は1点で交わる その点は外接円の中心を示す。 |
 |
|||||||||||||||||||||||||
| 三平方の定理 (ピタゴラスの定理) |
直角三角形において 斜辺c2=辺a2+辺b2 |
 |
|||||||||||||||||||||||||
三平方の定理の証明(ピタゴラスの定理の証明)例 |
|||||||||||||||||||||||||||
| ピタゴラスの数 | 直角三角形の3辺が整数になる組合せ(数)をピタゴラスの数という。
|
||||||||||||||||||||||||||
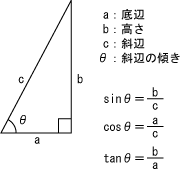
| 三角比 (三角関数) |
直角三角形の3辺の比(相似形)は、角θによって決まる。 この時の3辺の比を三角比と称する。 |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 正弦(sine・サイン) | sinθ=b/c sin0°=0 sin30°=1/2 sin45°=1/√2 sin60°=√3/2 sin90°=1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 余弦(cosine・コサイン) | cosθ=a/c cos0°=1 cos30°=√3/2 cos45°=1/√2 cos60°=1/2 cos90°=0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 正接(tangent・タンジェント) | tanθ=b/a tan0°=0 tan30°=1/√3 tan45°=1 tan60°=√3 tan90°=∞ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 正割(secant・セカント) | secθ=c/a | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 余割(cosecant・コセンカント) | cosecθ=c/b | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 余接(cotanjent・コタンジェント) | cotθ=a/b | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 三角比 (逆算三角関数) |
θ=sin-1b/c θ=cos-1a/c θ=tan-1b/a |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 三角比と三角関数 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 三角関数の符号 |  |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 三角関数 の公式 |
tanθ=sinθ/cosθ sin2θ+cos2θ=1 1+tan2θ=1/cos2θ |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2倍角の公式 | sin2θ=2sinθcosθ cos2θ=cos2θ−sin2θ=1−2sin2θ=2cos2θ−1 tan2θ=2tanθ/(1−tan2θ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 加法定理 | sin(A+B)=sinAcosB+cosAsinB sin(A−B)=sinAcosB−cosAsinB cos(A+B)=cosAcosB−sinAsinB cos(A−B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1−tanAtanB) tan(A−B)=(tanA−tanB)/(1+tanAtanB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 余弦定理 | a2=b2+c2−2bc cosA b2=c2+a2−2ca cosB c2=a2+b2−2ab cosC |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| 正弦定理 | a/sinA=b/sinB=c/sinC=2r r:外接円の半径 |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
弧度法 (ラジアン) |
角度を表す単位の一つ(単位記号:rad) 度(°)と同じように使用される。 360°=2π[rad] 1[rad]=360°/(2π) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 対応表 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
| 複素数の定義 (complex number) |
・複素数は、実数と虚数単位”j”の組合せ”a+jb”の形である数値を表す。 ・複素平面に図式化し、ベクトル計算を行う。 |
 |
|
| 虚数単位 (imaginary number) |
現実には存在しない値√(-1)の事を虚数単位という。 ・j=√(-1) ・j2=-1 ・j3=-j ・j4=1 ・(1/j)=-j |
||
| 公式 | ・(a+jb)+(c+jd)=(a+c)+j(b+d) ・(a+jb)−(c+jd)=(a−c)+j(b−d) ・(a+jb)×(c+jd)=(ac−bd)+j(bc+ad) ・(a+jb)/(c+jd)=(ac+bd)/(c2+d2)+j((bc−ad)/(c2+d2)) |
 |
|
| 複素平面 | ・縦軸に虚数(虚軸)、横軸に実数(実軸)を配した、複素数を表す平面を複素平面という。 ・複素平面上にベクトル図を描き、ベクトル合成(ベクトルの和・差)を行う。 |
 |
|
| ベクトル | ベクトル量 | 大きさだけを持つスカラ量(長さ、温度など)に対し、 大きさと方向を持つ量(力・速度等)をベクトル量という。 |
|
| 値の計算 | 複素平面に表したベクトル量は、実数、虚数の値から、三平方の定理(ピタゴラスの定理)で求める事ができる。 実際の値=√(実数2+虚数の数値2) ・皮相電力=有効電力(実数部)+j無効電力(虚数部) ・インピーダンス=コンダクタンス(実数部)+jサセプタンス(虚数部) |
 |
|
| ベクトルの和 | (a+jb)+(c+jd)=(a+c)+j(b+d) |  |
|
| ベクトルの差 | (a+jb)−(c+jd)=(a−c)+j(b−d) |  |
|
| このホームページの印刷に失敗する(1枚に収まらない)方のために (ホームページの印刷設定) |
| 進む | 株式会社 I.T.オフィス TOPページ |
| ・商用を除き、この資料(一連のホームページ・素材)を自由に流用してかまいません。・商用を除き、このホームページへのLINKは自由に行ってかまいません。(連絡は不要です)・本資料の使用・流用に関するいかなる損害も当社は一切の責任を負いませんのでご承知下さい。・本資料の著作権は株式会社 I.T.オフィスにあります。 担当:システム技術担当 伊藤( Mail:k.itou@itoffice.jp ) |